《图解算法》—二分法查找

概念

二分查找是一种算法，其输入是一个有序的元素列表(必须是有序的)，如果查找到的元素包含在列表中，二分查找返回其位置；否则返回null.

原理

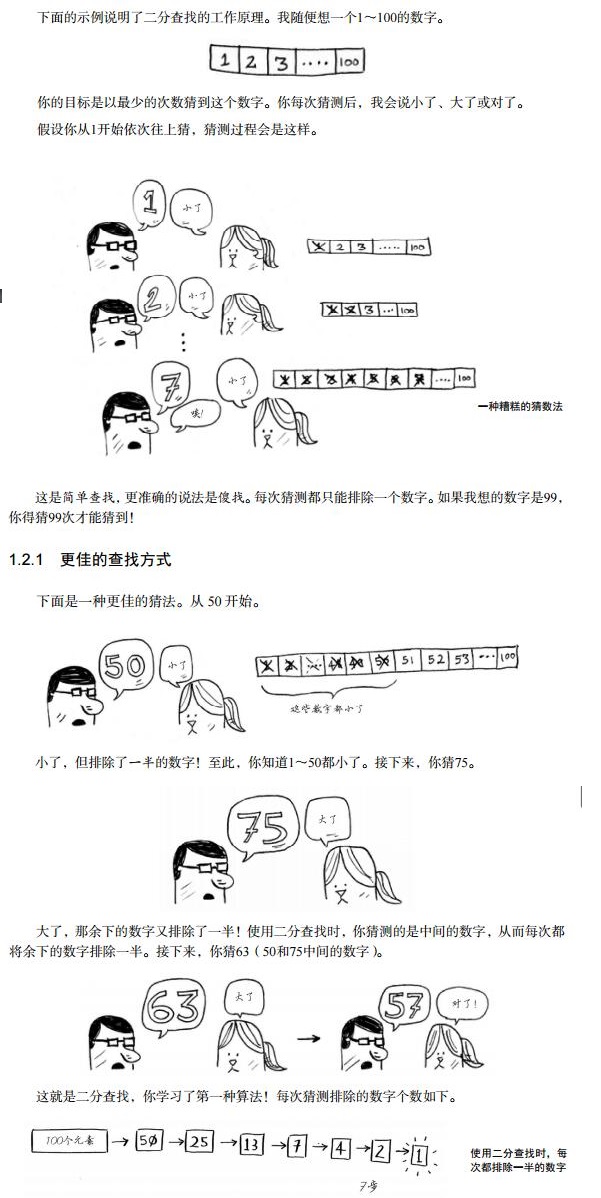
二分法原理

一般而言，对于包含n个元素的列表，用二分查找最多需要 $log_2n$ 步，而简单查找最多需要n步

例子：

函数binary_search接受一个ࣿ有序数组和一个元素。如果指定元素包含在数组中，这个函数将返回其位置，否则返回none。

代码

def binary_search(list, item):
    low = 0
    high = len(list) - 1
    while low <= high:
        mid = int((low + high) / 2)
        guess = list[mid]
        if guess == item:
            return mid
        if guess > item:
            high = mid - 1       # list[mid]值不是想要的值，在左区间
        else:
            low = mid + 1        # list[mid]值不是想要的值，在右区间
    return None
my_list = [1, 3, 5, 7, 9]
print(binary_search(my_list, 3))  # 找到，地址为1,索引从0开始
print(binary_search(my_list, -1))  # 没找到，返回none

小结：

二分查找的速度比简单查找快得多。
O(log n)比O(n)快。需要搜索的元素越多，前者比后者就快得越多。
算法运行时间并不以秒为单位。
算法运行时间是从其增速的角度度量的。
算法运行时间用大O表示法表示。